12. PID Implementation Solution

def run(robot, tau_p, tau_d, tau_i, n=100, speed=1.0):
    x_trajectory = []
    y_trajectory = []
    prev_cte = robot.y
    int_cte = 0
    for i in range(n):
        cte = robot.y
        diff_cte = cte - prev_cte
        prev_cte = cte
        int_cte += cte
        steer = -tau_p * cte - tau_d * diff_cte - tau_i * int_cte
        robot.move(steer, speed)
        x_trajectory.append(robot.x)
        y_trajectory.append(robot.y)
    return x_trajectory, y_trajectory

Ok. With the integral term we're keeping track of all the previous CTEs, initially we set int_cte to 0 and then add the current cte term to the count int_cte += cte . Finally we update the steering value, -tau_p * cte - tau_d * diff_cte - tau_i * int_cte with the new tau_i parameter.

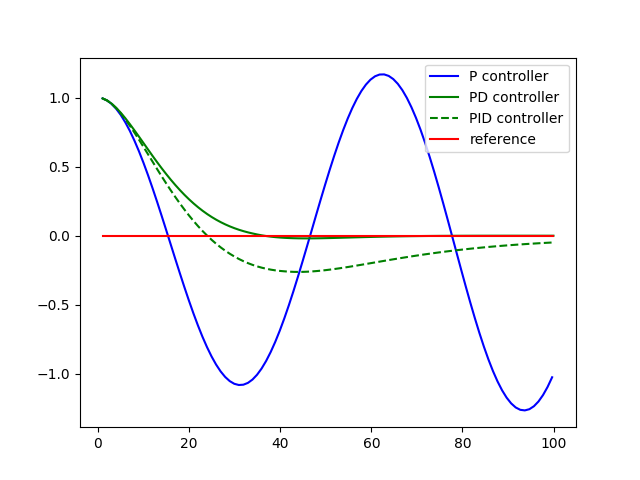
This may not seem all that impressive. PID seems to do worse than the PD controller! The purpose of the I term is to compensate for biases, and the current robot has no bias.

In the next programming quiz we'll add steering drift and revisit this graph.